Funciones

 FUNCIÓN GENERAL

Una función f: A  ⭢ B es una relación que asocia a cada elemento x ∈ A exactamente un elemento y ∈ B.

Definición normal

 

Una función f de A en B es un subconjunto de A x B tal que:

• Para todo x ∈ A, existe al menos un par (x,y) ∈ f.
• Si (x,y) ∈ f y (x,z) ∈ f, entonces y = z.

Notación:

f: A ⭢ B, x ↦ f (x)

• A es el dominio de f
• B es el codominio de f
• El conjunto {f(x) | x ∈ A} es el rango.

FUNCIÓN INYECTIVA

Una función es inyectiva si cada elemento del conjunto de llegada corresponde como máximo a un elemento del conjunto de partida.

Otra definición es la siguiente: una función f: A -> B es inyectiva, si no existen 2 elementos de A (conjunto de llegada) con una misma imagen. Veamos algunos ejemplos:

Para determinar si una función es inyectiva, tenemos que analizar la siguiente condición:

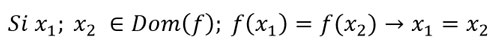
FUNCIÓN SOBREYECTIVA

Una función es sobreyectiva si cada elemento del conjunto de llegada (codominio) corresponde por lo menos a un elemento del conjunto de partida.

Otra definición más simple es la siguiente: una función es sobreyectiva si el rango es igual al conjunto de llegada o codominio. Veamos algunos ejemplos:

Para determinar si una función es sobreyectiva tenemos que determinar el rango. Por lo general, el conjunto de llegada es dato del problema. Si el rango que hemos hallado, es igual al conjunto de llegada, entonces se trata de una función sobreyectiva.

FUNCIÓN BIYECTIVA

Una función “f” es biyectiva si es inyectiva y sobreyectiva.

Otra definición es la siguiente: una función es biyectiva si cada elemento del conjunto de partida tiene una imagen distinta en el conjunto de llegada, y cada elemento del conjunto de llegada corresponde a un elemento del conjunto de partida.